Deriving Initial Conditions for an ODE |
bvalfit(v1, v2, x1, x2, xf, D, load1,
load2, scoreb)
sbval(v1, x1, x2, D, load1, scorei)
Returns a vector containing those initial values left unspecified at
x1 for the ODE or system of ODEs identified in
D. These initial values can then be used in one of the
ODE solvers. If you know some values of
the solution and its first n − 1 derivatives
at an intermediate value, use bvalfit. If you know some values
at the initial and terminal points, use sbval. The boundary value
problem is converted to an initial value problem by shooting from the
endpoints and matching the trajectories of the solution and its derivatives
at an intermediate point.
Arguments:
- v1, v2
are vectors of real guesses for the initial values left unspecified at
x1.
- x1, x2
are the real endpoints of the interval on which the solution to differential
equations is evaluated.
- xf is a real intermediate
point between x1 and x2
at which the trajectories of the solutions are constrained to be equal.
-
D(x, y)
is an n-element vector-valued function of the
independent variable, x, and a vector of functions,
y, containing the equations for the first derivatives
of all unknown functions in the system of ODEs. To create this vector,
cast your equation(s) with a first derivative term by itself on the left-hand-side,
with no multipliers, and no higher order derivatives in the equation.
For example, a single ODE of the function y(x)
which contains a second derivative must be written as a system of equations
in y0(x) and y1(x),
where the first derivative of y0 is
y1. The single- function ODE
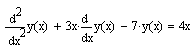
is rewritten for the solver, using vector
subscripts, as
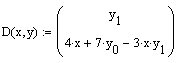 with implied left-hand-side
with implied left-hand-side
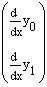
- load1(x1, v1), load2(x2, v2) are real vector-valued functions whose elements
correspond to the values of yn at x1 and x2, respectively. Some
of these values are known initial conditions. Unknown values are set
to corresponding guess values from v1 and v2,
respectively.
- scoreb(xf, y) is
a real vector-valued function used to specify how you want the solutions
to match at xf. Usually you need to define score(xf,
y) := y to make the solutions to all unknown functions match up
at xf.
- scorei(x2, y) is
a real vector-valued function having the same number of elements as v. Each element is the difference between an initial condition
at x2, as originally specified, and the corresponding
estimate from the solver. The score vector measures how closely a proposed
solution matches the initial conditions at x2.
A value of 0 for any element indicates a perfect match.
Notes:

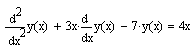
with implied left-hand-side

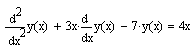
with implied left-hand-side
