Final-Value Ordinary Differential Equation Solvers

These functions are deprecated. Please use or switch to the uppercase ODE solvers or an ODE solve block. We expect to support these functions only for the next two versions of Mathcad.

The properties of each of these solvers are the same as the corresponding uppercase functions, but they calculate fewer values of the solution. Instead of specifying the number of points in the result, specify the level of accuracy, and allow the functions to generate a solution at the required number of points along the interval.

bulstoer(init, x1, x2, acc, D, kmax, s) Smooth systems using the Bulirsch-Stoer method.
rkadapt(init, x1, x2, acc, D, kmax, s) Fourth-order Runge-Kutta with adaptive step size.

stiffb(init, x1, x2, acc, D, J, kmax, s) uses the Bulirsch-Stoer method for stiff systems.
stiffr(init, x1, x2, acc, D, J, kmax, s) uses the Rosenbrock method for stiff systems.
radau(init, x1, x2, acc, D, kmax, s) uses the RADAU5 method for stiff systems.

Each of these functions returns a matrix in which the first column contains, at minimum, x1 and x2, and subsequent columns contain the corresponding values of the solution(s) to the nth-order ODE(s), and the n − 1 derivatives of the solution(s).

Arguments:

• init is either a vector of n real initial values or a single scalar initial value, in the case of a single ODE.
• x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) will be evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
• acc is a real, scalar accuracy. Small acc forces smaller steps along the solution trajectory, increasing the accuracy of the solution. Values of acc around 0.001 generally yield accurate solutions.
• D(x,y) is an n-element vector-valued function of the independent variable, x, and a vector of functions, y, containing the equations for the first derivatives of all unknown functions in the system of ODEs. To create this vector, cast your equation(s) with a first derivative term by itself on the left-hand-side, with no multipliers, and no higher order derivatives in the equation. For example, a single ODE of the function y(x) which contains a second derivative must be written as a system of equations in y₀(x) and y₁(x), where the first derivative of y₀ is y₁. The single-function ODE

  

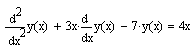
  is rewritten for the solver, using vector subscripts, as

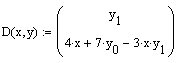  with implied left-hand-side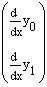

• J is a function which returns an n × (n + 1) matrix of partial derivatives of the system of equations in D. The first column contains the derivatives with respect to x; the remaining columns form the Jacobian matrix (partials with respect to y_n) for the system of differential equations. For the example above, the matrix J is

  

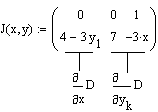
• kmax ≥ 2 is the integer number of intermediate points at which the solution will be approximated.
• s is the minimum real, positive spacing between intermediate x-values at which the solutions are to be approximated.

Notes:

• The number of intermediate values returned depends on a combination of acc, kmax and s.
• The functions D and J are provided to the solver without their arguments, and the functions y_n(x) are specified in D and J without their argument. The second argument to D and J must be subscripted as a vector, even if there is only a single entry.
• You may wish to use ODE Solve Blocks to simplify the entry of your equations and initial conditions.